
Quadratic Transformer: Warm-Up
It's always a good idea to "warm up" or acquaint yourself with a new software tool before using it with an activity. If you feel comfortable exploring the buttons and features on your own, feel free to do that. If you prefer a more structured exploration, try the activities below.
Click to launch the Quadratic Transformer.
Note The
Quadratic Transformer opens in a new browser window. As you explore the
software, keep this window open for reference.
Warm-up A: Getting Started
First, let's get the lay of the land.
- Familiarize yourself with the buttons on the right side of
the screen. Can you guess what each button does? What functionality do
the buttons on the top provide?
- Find the symbolic expression at the bottom of the screen. This is the expression for a quadratic function. What function does the program display when it opens?
Warm-Up B: Try It and See
- The Slider. Move the slider (the inverted
triangle at the bottom of the graph). What does it do? Use the slider
to find the vertex of the starting parabola and a few points on it.
- New Function. Click the New button and you'll see a new parabola. Where did the first one go?
In the list of symbolic expressions on the right, can you tell which
expression represents which parabola? What happens to a parabola when
you click its graph? How about when you click its expression in the
table? This is how you choose the parabola you want to work with.
- The Expression.
Look at the symbolic expression (displayed in polynomial form by
default) at the bottom of the screen. Click the box in front of
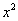 (representing the value of the coefficient a) to select it. Notice what happens when you click the up and down arrows a few times. Which parabola changes? How?
(representing the value of the coefficient a) to select it. Notice what happens when you click the up and down arrows a few times. Which parabola changes? How?

Choose a parabola you want to change (by clicking its color in the list at the right). Click the box in front of the x term to select it. Notice how the parabola and
the symbolic expression change when you click the up and down arrows a
few times. Do the same with the last box (the constant term). What do
you notice now?
- Experiment. Try the other buttons. Each
time you try a new button, see what changes you notice—in the parabola,
in the symbolic expression (at the bottom), and in the list of symbolic
expressions at the right. Watch what the slider does too.
When you're satisfied with how the buttons work, try the next warm-up.
Warm-Up C: Observing Several Parabolas
Now you're ready to use what you've learned about the software to
work with some parabolas that share common characteristics. See what
you notice.
Note To clear the screen at any time, click Delete All.
- Make three parabolas whose vertices are all on the y-axis. What do their symbolic expressions have in common?
- Make two parabolas that are mirror images of each other. What do you notice about their symbolic expressions?
- Make the parabola
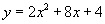 .
.
What are the coordinates of its vertex? Click the vertex form for the
symbolic expression. Are you correct? How do you know?
- Make the parabola
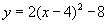 .
.
Then make a second parabola that crosses the x-axis at the same points as the first. Compare the vertices of these two parabolas.
- Make a parabola with its vertex at (12, 0).
Note
Use the Change X Scale button to make the parabola easier to see.
First, click the Change X Scale button. Place the mouse anywhere over
the graph, and drag the cursor left or right until you are satisfied
with the scale. Click Change X Scale again to return to the usual view.
- Use the Duplicate button to make
a second parabola. Now change the vertex so that the new parabola
intersects the original parabola. Then find the intersection point(s). (Hint: How can the slider help you?)
Note
Most of the activities in this course can be done in the Quadratic
Transformer's main window. However, you might want to try some of the
tasks again using the Transform Function button. It opens the Function
Transformation window, which allows you to transform functions in
different ways. Feel free to explore this window on your own. Full
directions are in the Quadratic Transformer User Guide in Resources, Interactive: Quadratic Transformer.
Warm-Up D: More Parabolas
Try the additional activities below, still using the Quadratic Transformer.
Note You might want to try using the Transform Function button for these activities. It opens a second window with slightly different attributes. Full directions are in the Quadratic Transformer User Guide in Resources, Interactive: Quadratic Transformer.
- Make the parabola
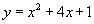 .
.
What are the coordinates of its vertex?
Find two ways to check if you are correct.
- Make a parabola with its vertex at (1, -14).
Then make a second parabola that has a different vertex but crosses the first parabola.
What is/are the intersection point(s)?

