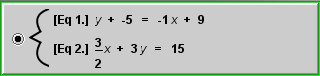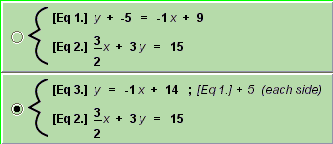System Solver: Warm-Up
It's always a good idea to "warm up" or acquaint yourself with a new software tool before using it with an activity. If you feel comfortable exploring the buttons and features on your own, feel free to do that. If you prefer a more structured exploration, try the activities below.
Click to open the System Solver.
Note The System Solver opens in a new browser window. As you explore the software, keep this window open for reference.
As you navigate through the System Solver's screens and dialog
boxes, familiarize yourself with the elements of each. How many buttons
are there? What guesses can you make about what they do? What other
controls or data entry fields are on the screen?
Warm-Up A: Entering the system
In the following tasks, you will enter the system 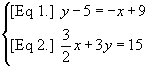
When you open the System Solver, a window for entering the system
you want to solve is displayed. Note how there are two areas of the
screen where you can enter an equation in the system. You'll see how to
use different equation formats. You must enter coefficients and
constants as fractions, so remember to set the denominator as well as
the numerator.

In order to enter this system, you'll need to choose a different equation format than 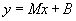 , which is the default equation format. You'll also input the values for coefficients and constants in the system.
, which is the default equation format. You'll also input the values for coefficients and constants in the system.
- Under Equation 1, click on the default equation format (
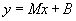 ) to display the other formats.
) to display the other formats.
These formats allow you to enter most systems you're likely to encounter.
- Select the appropriate format for Equation 1.
- Click the down arrows
 next to any coefficient or constant to select a value from the menu. (The down arrow
next to any coefficient or constant to select a value from the menu. (The down arrow  button always indicates a selectable menu.)
button always indicates a selectable menu.)
- Note the range of values selectable in this way.
- You can also manually enter a specific value, including a negative number, by simply typing it into the box.
- Enter the coefficients and constants to complete Equation 1.
- Follow the same steps for entering Equation 2.
- Remember, you cannot enter decimals such as
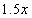 . You must enter decimals as
. You must enter decimals as 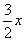 . The System Solver only allows rational numbers.
. The System Solver only allows rational numbers.
- Check your entries for the system and click Start Solving.
After you click Start Solving, the display where
you've been entering the system is replaced by another screen, on which
you can solve the system, and view it in symbolic, graphic, and tabular
formats.
Warm-Up B: Exploring the Solver
Before performing any operations to solve the system—you'll do that shortly—take some time to explore this new screen.
- Find the three main areas of the screen: symbolic, graphic, and tabular.
Symbolic
- Notice
that the symbolic representation of the system uses the convention of a
bracket to designate both equations in the system.
- Notice that each equation in the symbolic representation is labeled with an equation number for reference purposes.
For example, [Eq 1].
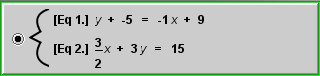
- Notice the buttons under the symbolic side of the screen. You'll use these later to work on the system.

Graphic
- Which equations do you think the thick gray lines in the graph represent?
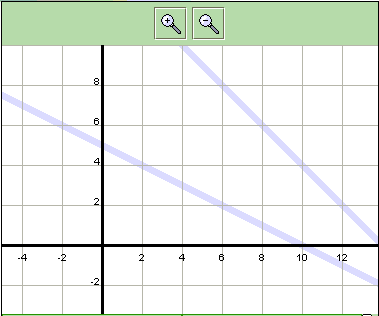
Tabular
- Try dragging the scroll bar to display more values for each equation in the system.

- Click and drag on the graph to display the point where the two lines intersect.
- Notice
that the arrow cursor changes to a hand anytime it is positioned over
the graph. This indicates that you can drag the graph.
- Move the slider bar that is on the right side of the tabular area by clicking or dragging.
- How does moving the slider bar change the table?
- How does moving the slider bar change the graph?
- How can you tell which line in the graph corresponds to which table of values?
- What changes in the tables and in the graph when you slide the bar to display the row with the values x = 28 and y = −14? Find two differences in each.
- What does the selected row in the table and the selected point on the graph represent?
Warm-Up C: Solving the System
Using the System Solver is not the fastest way to solve a system of
linear equations. That's because it was designed to slow down the
process so you can focus your attention on the intermediate steps.
- Click Operate on Both Sides.
- Which equation in the system is selected when the dialog box opens?
- How do you select the other equation?
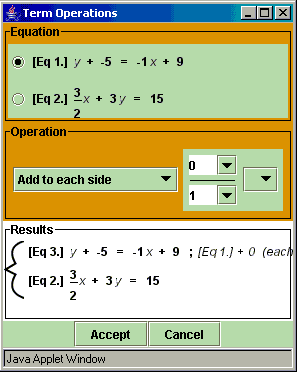
- For this step, do not enter any values or click Accept until instructed to do so in Step 3. Explore the Operation area of this dialog box to determine what operations you can perform on the equation. The down arrow
 button indicates a selectable menu.
button indicates a selectable menu.
- Could you subtract 5 from both sides?
- Could you add or subtract 5x to or from each side?
- Could you multiply/divide each side by 5?
- Could you multiply/divide each side by 5x?
- Now, add 5 to both sides of Equation 1 and click Accept.
- Notice that a new system appears and is selected.
- Notice that the new equation is labeled Equation 3, and that Equation 3 has replaced Equation 1 in the system.
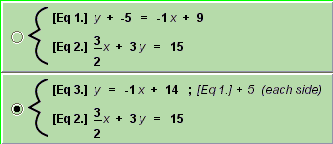
-
Before you continue solving the system, check out what happens when you
move the slider bar to the right of the tabular area all the way down
and up again.
- Which system is now represented by the table and graph?
- Click Combine Equations.
- When the Combine Equations dialog box appears, select Substitute from the pull-down menu.
- Click on the equations, which will display a pull-down menu, so that Equation 3 is substituted into Equation 2.
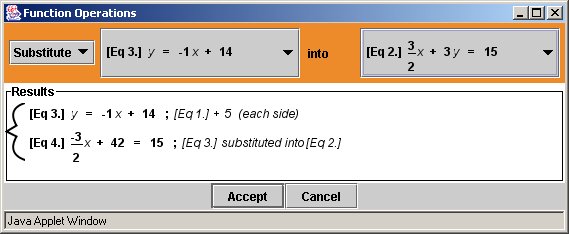
- Click Accept and the main window will reappear

- Which equation in the previous system has been replaced by another in the new system?
- Whenever
you Combine Equations, it is the second equation in the Combine
Equations dialog box that gets replaced in the new system by a new
equation.

- Notice
that, although you combined the equations in the previous system, the
System Solver displays a new system as the result of the operation. You may not have expected that the top equation (Equation 3), would still be part of the system, but it is!
- Move the slider bar to the right of the tabular area down and up again.
- Notice how Equation 4 is shown in the graph and the table.
- Continue solving the system until you are comfortable using the System Solver.


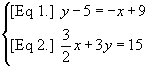

![]() , which is the default equation format. You'll also input the values for coefficients and constants in the system.
, which is the default equation format. You'll also input the values for coefficients and constants in the system.